R语言—支持向量机(SVM)
阿狸的Blog · 2021-08-27
今天,第一次尝试用R Markdown来写学习笔记,这是一个边学边记录的过程,今天的内容是支持向量机(Support Vector Machines),简称SVM。
数据集介绍
今天用到的还是R包自带的”iris”数据集,下面我们导入数据:
data("iris")查看前六行:
str(iris)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
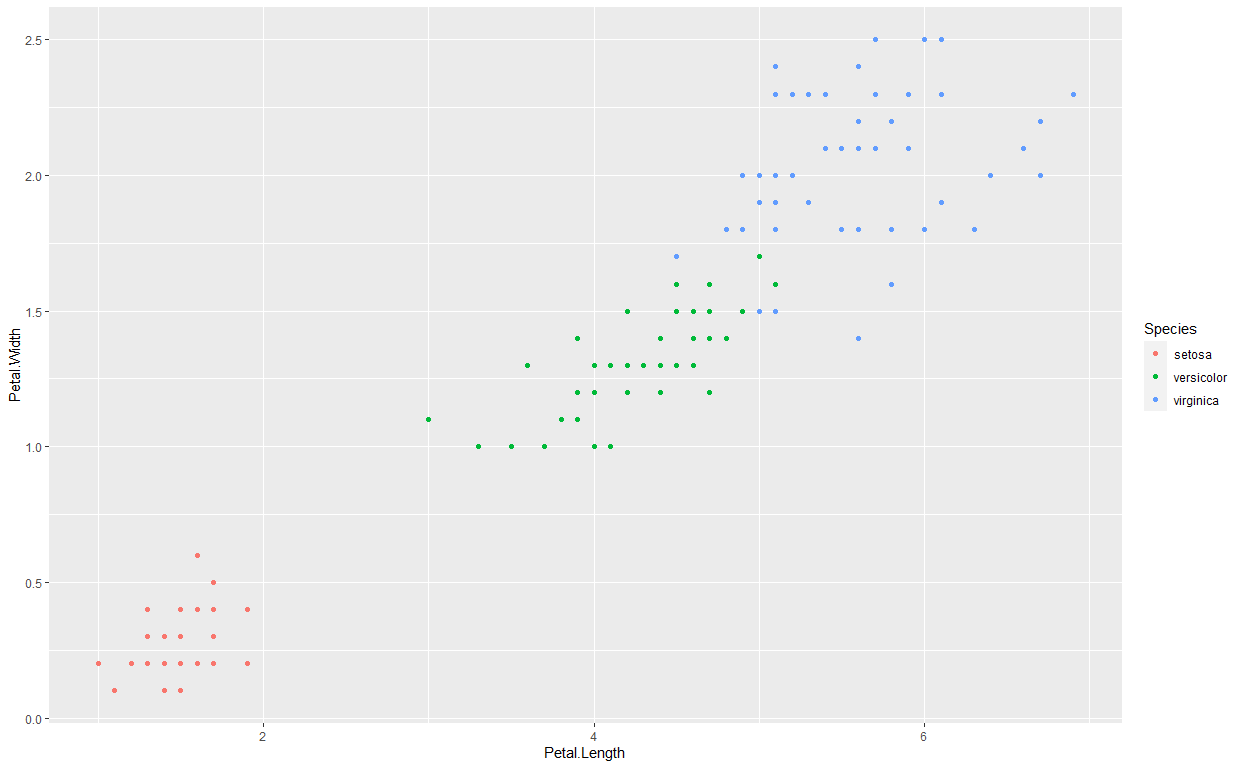
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...数据集可视化:调用qplot函数绘制散点图,其中Petal.Length为x轴,Petal.Width为y轴:
library(ggplot2)qplot(Petal.Length,Petal.Width,data = iris,
color=Species)
20210827234155
支持向量机
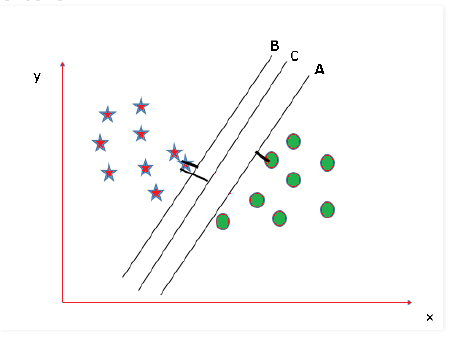
SVM用于分析用于分类和回归分析的数据。它主要用于分类问题。在该算法中,每个数据项被绘制为n维空间中的一个点(其中n是特征的数量),每个特征的值是特定坐标的值。然后,通过寻找最能区分这两类的超平面来执行分类。
20210827210511
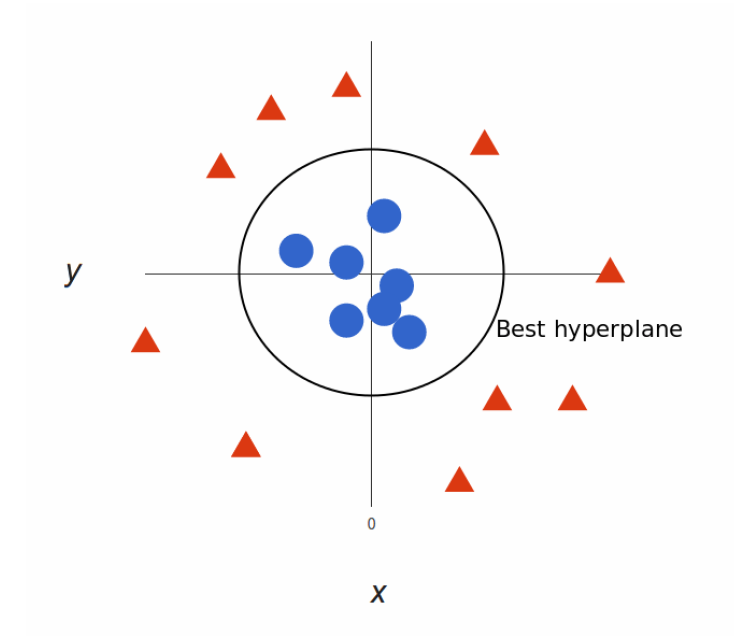
除了执行线性分类之外,SVM可以有效地执行非线性分类。
20210827211244
在SVM的众多packages中,台湾⼤学林智仁⽼师开发的LIBSVM最常用,也就是下面要用到的”e1071”包。
library(e1071)用svm函数来建立模型:
mymodel <- svm(Species~.,data=iris)
summary(mymodel)##
## Call:
## svm(formula = Species ~ ., data = iris)
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 1
##
## Number of Support Vectors: 51
##
## ( 8 22 21 )
##
##
## Number of Classes: 3
##
## Levels:
## setosa versicolor virginica分析数据可以看出:
SVM-分类机:C-classification。共五种:C-classification,nu-classification,one-classification(for novelty detection) ,eps-regression, nu-regression。
SVM-核函数:radial。共四类:线性核函数(linear)、多项式核函数(polynomial)、径向基核函数(radial basis,RBF)和神经网络核函数(sigmoid)。
cost:1。C分类中惩罚项c的取值。
支持向量的数量是51。
模型可视化:
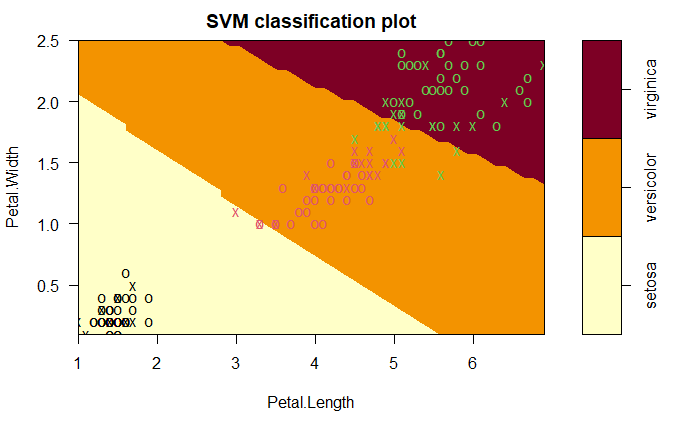
plot(mymodel,data = iris,
Petal.Width~Petal.Length,
slice = list(Sepal.Width = 3, Sepal.Length = 4))
20210827234727
因为整个数据集有4个变量,这里我门把Sepal.Width = 3, Sepal.Length = 4,即设定为固定值。
每种颜色代表一个物种的类别(setosa/versicolor/virginica)。其中8个属于setosa。浅黄色图中共有8个”×”
混淆矩阵
我们将使用创建的模型来预测每个物种。
pred <- predict(mymodel,iris)
tab <- table(Predicted = pred,Actual = iris$Species)
tab## Actual
## Predicted setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 48 2
## virginica 0 2 48从表中可以看出,有50个点属于物种setosa,48个属于versicolor,这里有2个被预测成了virginica。我们来计算一下总的错误率。
1-sum(diag(tab))/sum(tab)## [1] 0.02666667约为2.7%,改模型使用径向基核函数(radial)为核心。下面我们来尝试应用其他核函数:线性核函数(linear)、多项式核函数(polynomial)和神经网络核函数(sigmoid)。
- 线性核函数(linear)错误率:
mymodel <- svm(Species~.,data=iris,kernel = "linear")
summary(mymodel)##
## Call:
## svm(formula = Species ~ ., data = iris, kernel = "linear")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: linear
## cost: 1
##
## Number of Support Vectors: 29
##
## ( 2 15 12 )
##
##
## Number of Classes: 3
##
## Levels:
## setosa versicolor virginicaplot(mymodel,data = iris,
Petal.Width~Petal.Length,
slice = list(Sepal.Width = 3, Sepal.Length = 4))
pred <- predict(mymodel,iris)
tab <- table(Predicted = pred,Actual = iris$Species)
tab## Actual
## Predicted setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 46 1
## virginica 0 4 491-sum(diag(tab))/sum(tab)## [1] 0.03333333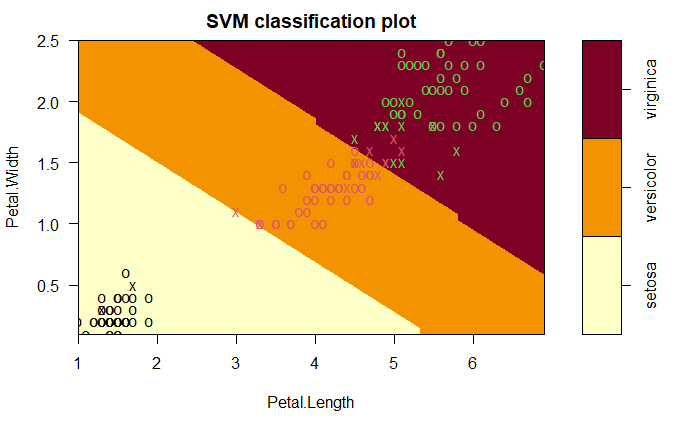
20210827234824
这里错误率是3.3%,较radial增加。
- 多项式核函数(polynomial)及错误率:
mymodel <- svm(Species~.,data=iris,kernel = "polynomial")
summary(mymodel)##
## Call:
## svm(formula = Species ~ ., data = iris, kernel = "polynomial")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: polynomial
## cost: 1
## degree: 3
## coef.0: 0
##
## Number of Support Vectors: 54
##
## ( 6 26 22 )
##
##
## Number of Classes: 3
##
## Levels:
## setosa versicolor virginicaplot(mymodel,data = iris,
Petal.Width~Petal.Length,
slice = list(Sepal.Width = 3, Sepal.Length = 4))
pred <- predict(mymodel,iris)
tab <- table(Predicted = pred,Actual = iris$Species)
tab## Actual
## Predicted setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 50 7
## virginica 0 0 431-sum(diag(tab))/sum(tab)## [1] 0.04666667 这里错误率是4.7%,较
这里错误率是4.7%,较radial增加。
- 神经网络核函数(sigmoid)及错误率:
mymodel <- svm(Species~.,data=iris,kernel = "sigmoid")
summary(mymodel)##
## Call:
## svm(formula = Species ~ ., data = iris, kernel = "sigmoid")
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: sigmoid
## cost: 1
## coef.0: 0
##
## Number of Support Vectors: 54
##
## ( 6 26 22 )
##
##
## Number of Classes: 3
##
## Levels:
## setosa versicolor virginicaplot(mymodel,data = iris,
Petal.Width~Petal.Length,
slice = list(Sepal.Width = 3, Sepal.Length = 4))
pred <- predict(mymodel,iris)
tab <- table(Predicted = pred,Actual = iris$Species)
tab## Actual
## Predicted setosa versicolor virginica
## setosa 49 0 0
## versicolor 1 41 7
## virginica 0 9 431-sum(diag(tab))/sum(tab)## [1] 0.1133333 这里错误率是11.3%,较
这里错误率是11.3%,较radial增加。在所有核函数中性能最差。
模型的调整(超参数优化)
这里我们使用tune()函数来及逆行调整。
set.seed(124)
tmodel <- tune(svm,Species~.,data = iris,
ranges = list(epsilon = seq(0,1,0.1,),
cost = 2^(2:9)))这里使用从0开始,并以0.1递增的序列。即我们将有11个不同的值: epsilon:0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0。
另一个需要微调的参数是cost。这个值太大会导致过拟合。太小会导致拟合不足。所以使用较大的范围,以便能够获得最佳。即我们将有8个不同的值:
cost:22,23,24,25,26,27,28,29。
这样就会得到:11×8种组合。组合越多,可能需要的时间就越长。
绘制tmodel:
plot(tmodel)
 参数对应较暗的区域意味着更好的结果在这些区域。根据图示我们可以缩小一下
参数对应较暗的区域意味着更好的结果在这些区域。根据图示我们可以缩小一下cost的范围:
set.seed(124)
tmodel <- tune(svm,Species~.,data = iris,
ranges = list(epsilon = seq(0,1,0.1,),
cost = 2^(2:7)))
plot(tmodel)
 我们来看看tmodel的摘要:
我们来看看tmodel的摘要:
summary(tmodel)##
## Parameter tuning of 'svm':
##
## - sampling method: 10-fold cross validation
##
## - best parameters:
## epsilon cost
## 0 8
##
## - best performance: 0.03333333
##
## - Detailed performance results:
## epsilon cost error dispersion
## 1 0.0 4 0.04000000 0.04661373
## 2 0.1 4 0.04000000 0.04661373
## 3 0.2 4 0.04000000 0.04661373
## 4 0.3 4 0.04000000 0.04661373
## 5 0.4 4 0.04000000 0.04661373
## 6 0.5 4 0.04000000 0.04661373
## 7 0.6 4 0.04000000 0.04661373
## 8 0.7 4 0.04000000 0.04661373
## 9 0.8 4 0.04000000 0.04661373
## 10 0.9 4 0.04000000 0.04661373
## 11 1.0 4 0.04000000 0.04661373
## 12 0.0 8 0.03333333 0.04714045
## 13 0.1 8 0.03333333 0.04714045
## 14 0.2 8 0.03333333 0.04714045
## 15 0.3 8 0.03333333 0.04714045
## 16 0.4 8 0.03333333 0.04714045
## 17 0.5 8 0.03333333 0.04714045
## 18 0.6 8 0.03333333 0.04714045
## 19 0.7 8 0.03333333 0.04714045
## 20 0.8 8 0.03333333 0.04714045
## 21 0.9 8 0.03333333 0.04714045
## 22 1.0 8 0.03333333 0.04714045
## 23 0.0 16 0.03333333 0.04714045
## 24 0.1 16 0.03333333 0.04714045
## 25 0.2 16 0.03333333 0.04714045
## 26 0.3 16 0.03333333 0.04714045
## 27 0.4 16 0.03333333 0.04714045
## 28 0.5 16 0.03333333 0.04714045
## 29 0.6 16 0.03333333 0.04714045
## 30 0.7 16 0.03333333 0.04714045
## 31 0.8 16 0.03333333 0.04714045
## 32 0.9 16 0.03333333 0.04714045
## 33 1.0 16 0.03333333 0.04714045
## 34 0.0 32 0.05333333 0.07568616
## 35 0.1 32 0.05333333 0.07568616
## 36 0.2 32 0.05333333 0.07568616
## 37 0.3 32 0.05333333 0.07568616
## 38 0.4 32 0.05333333 0.07568616
## 39 0.5 32 0.05333333 0.07568616
## 40 0.6 32 0.05333333 0.07568616
## 41 0.7 32 0.05333333 0.07568616
## 42 0.8 32 0.05333333 0.07568616
## 43 0.9 32 0.05333333 0.07568616
## 44 1.0 32 0.05333333 0.07568616
## 45 0.0 64 0.05333333 0.07568616
## 46 0.1 64 0.05333333 0.07568616
## 47 0.2 64 0.05333333 0.07568616
## 48 0.3 64 0.05333333 0.07568616
## 49 0.4 64 0.05333333 0.07568616
## 50 0.5 64 0.05333333 0.07568616
## 51 0.6 64 0.05333333 0.07568616
## 52 0.7 64 0.05333333 0.07568616
## 53 0.8 64 0.05333333 0.07568616
## 54 0.9 64 0.05333333 0.07568616
## 55 1.0 64 0.05333333 0.07568616
## 56 0.0 128 0.06000000 0.07336700
## 57 0.1 128 0.06000000 0.07336700
## 58 0.2 128 0.06000000 0.07336700
## 59 0.3 128 0.06000000 0.07336700
## 60 0.4 128 0.06000000 0.07336700
## 61 0.5 128 0.06000000 0.07336700
## 62 0.6 128 0.06000000 0.07336700
## 63 0.7 128 0.06000000 0.07336700
## 64 0.8 128 0.06000000 0.07336700
## 65 0.9 128 0.06000000 0.07336700
## 66 1.0 128 0.06000000 0.07336700这里的方法是10倍交叉验证:10-fold cross validation 。 最佳表现是:0.03333333。
最佳模型
mymodel <- tmodel$best.model
summary(mymodel)##
## Call:
## best.tune(method = svm, train.x = Species ~ ., data = iris, ranges = list(epsilon = seq(0,
## 1, 0.1, ), cost = 2^(2:7)))
##
##
## Parameters:
## SVM-Type: C-classification
## SVM-Kernel: radial
## cost: 8
##
## Number of Support Vectors: 35
##
## ( 6 15 14 )
##
##
## Number of Classes: 3
##
## Levels:
## setosa versicolor virginica可以看到最佳模型的各种参数。
模型可视化:
plot(mymodel,data = iris,
Petal.Width~Petal.Length,
slice = list(Sepal.Width = 3, Sepal.Length = 4))

最佳模型的混淆矩阵及分类错误
pred <- predict(mymodel,iris)
tab <- table(Predicted = pred,Actual = iris$Species)
tab## Actual
## Predicted setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 48 0
## virginica 0 2 501-sum(diag(tab))/sum(tab)## [1] 0.01333333这里错误率是1.3%,真的是最佳。150个点只有2个被错误分类。比之前的要少的多。
